Comparing Classification Models
Contents
Comparing Classification Models¶
So right now our model is just a line that classifies points on its right as risks and points on its left as not. But our model doesn’t have to be this way. Another model we might use is the nearest-neighbors model: given a point, find the training point that is closest to it and use that neighbor’s classification as its own. With this we make the big assumption that similar points (in terms of the features we’re using, income and balance) will be close together.
Which one should we use? Let’s compare the behavior of the nearest-neighbor classifier (left) to that of a linear classifier (right).
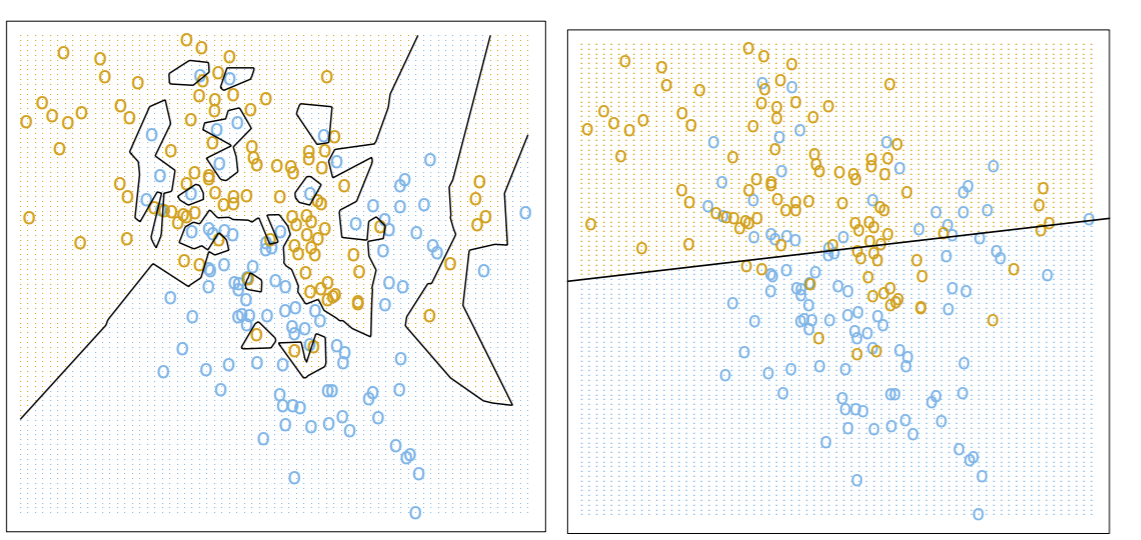
The obvious advantage of the NN-classifier is that it always predicts training data correctly: in other words, 100% training accuracy. Another way to think about this: if our test point was the same exact point as one of our training points, it would always be classified correctly. This is a good thing, right? If 100% is good for human learning in school, it’s gotta be also good for machine learning, right?
Right?
Overfitting and Underfitting¶
NO. In real life, nobody gives a shit if our program can correctly classify points we already know the answers to. The best models all have good test accuracy: they predict new and unseen data’s classes well before the fact.
Note the decision boundary for the NN-classifier is all fucked up- and probably won’t do the greatest job at predicting new data because of it. There’s a special machine learning term for this: overfitting. Whenever you see these weird scribbly decision boundaries, it’s usually a good sign you might be overfitting to your data. At the same time, if your classifier isn’t complex enough (or uses badly chosen features) to make nuanced predictions (think of a model that only uses height to predict someone’s credit risk), we call this underfitting.
The goal, of course, is to find the perfect balance between overfitting and underfitting: our model must be complex enough to estimate the true relationship between data points, but it can’t be TOO closely fit on our training data, or it won’t generalize to testing data well at all.
Look at the linear classifier’s accuracy (on the right). The training accuracy is actually pretty bad: there’s a lot of blue points in the left region where yellow is being predicted. Same for the yellow points in the blue region. But the decision boundary is less complex, so it might generalize to unseen data better.
Which one to use? No right answer - it depends the context and other factors. We have to just analyze the cases where each classifier works best and try to match it with the prediction problem we have at hand. But now we know what makes a good classifier- and that’s gonna be very helpful towards choosing one.
What if we adjust the NN algorithm so that instead of a single nearest neighbor, we pick the 15 nearest neighbors and classify our test point based on the majority class of those 15 neighbors? Well then we get this much less janky decision boundary:
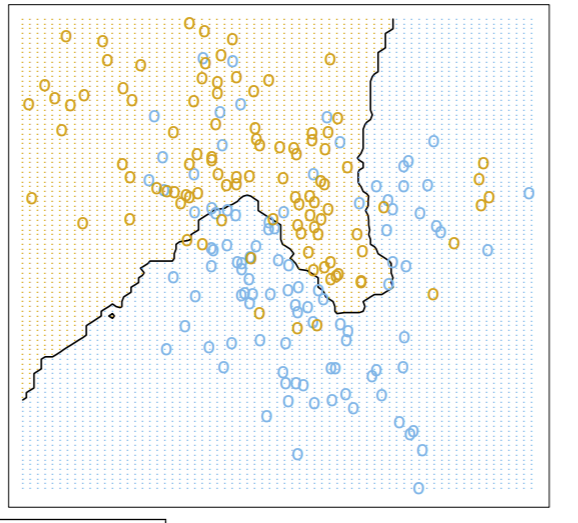
So even though we misclassify a lot more training points, like with the linear decision boundary, we can expect this model to generalize (predict unseen data) much better. In effect, we reduce overfitting because we’re now considering a lot of points around us rather than just one.
