Linear Separability of Data
Linear Separability of Data¶
Data is linearly separable if there exists a hyperplane that separates all the sample points in class C from all not in class C. Basically, if you can make a wall that completely separates one kind of points from the other, the data is linearly separable.
The below figure, for example, has data that is linearly separable because we have a line that separates the blue points from red:
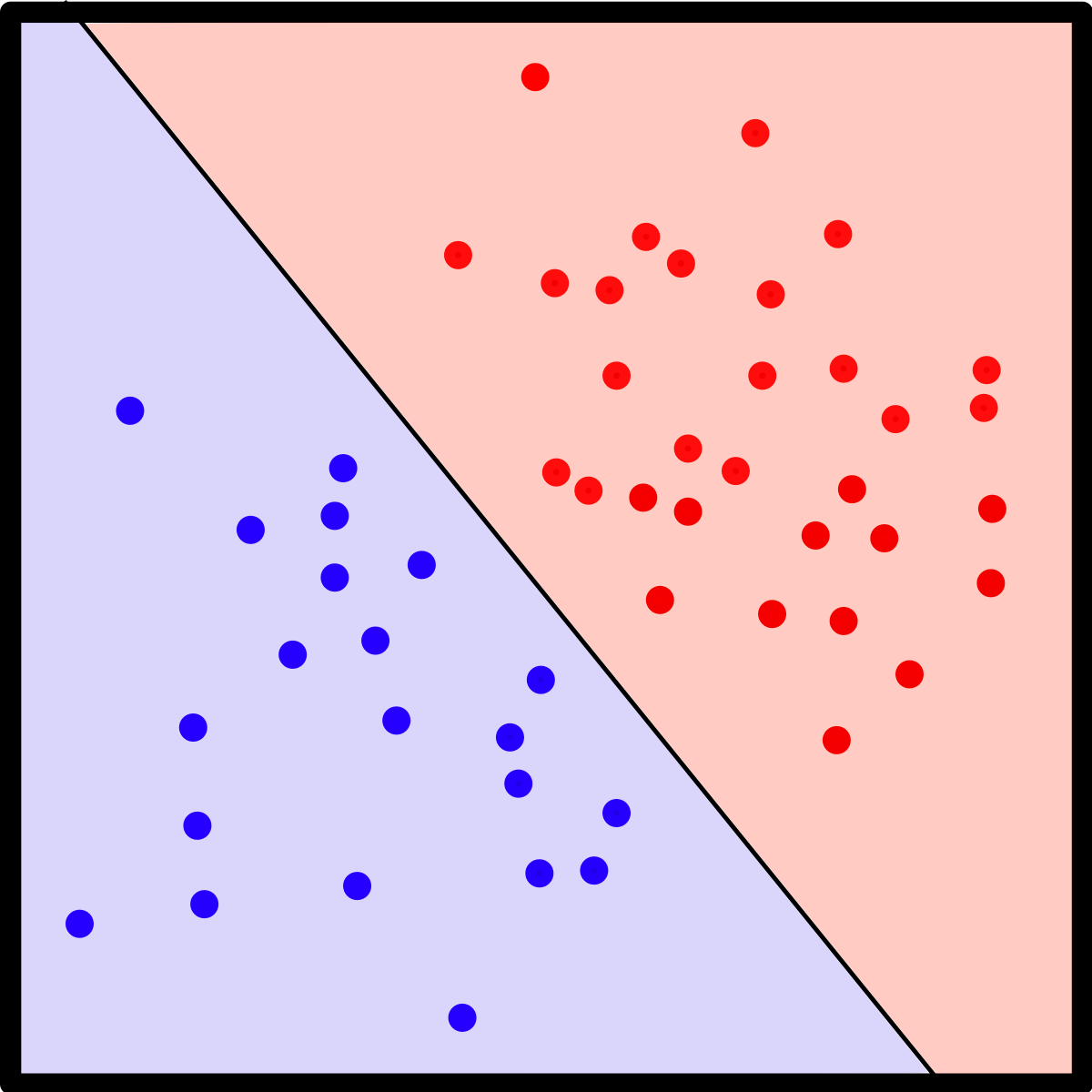
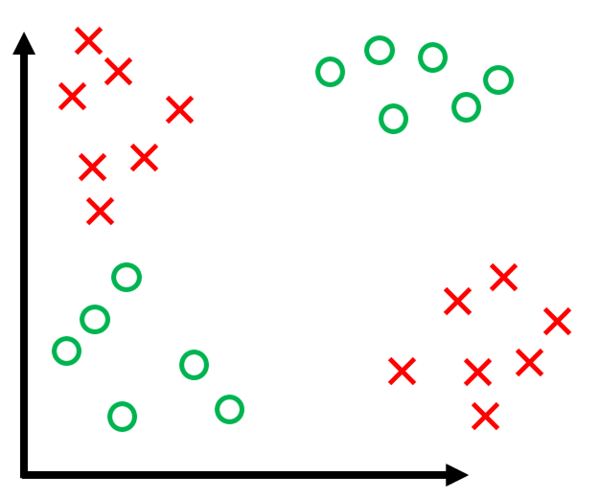
Note that the linear in “linearly separable” is very important. Data that is clearly separable might not be linearly separable. For example, in the below graph you can clearly make out the groups where the green X’s and red O’s are. However, I’ll bet you my Tesla that you can’t draw a line that linearly separates the data: all the green on one side of the line, and all the red on the other.
Some algorithms only work on linearly separable data- like SVMs. SVMs are rarely used in practice but are good instructional tools for understanding the basics of linear classifiers.
Note
Most real-world data is not linearly separable: we will always have outliers and points that just push past the decision boundary. Linear classifiers thus probably won’t have perfect training accuracy, but it can still definitely generalize well to unseen data, which we know is the most important thing.
