Validation
Validation¶
We already know the two big steps in machine learning is training and testing. However, there is actually a third in-between step: validation. Validation is the best means of deciding the arbitrary choices in machine learning:
Which algorithm to use (nearest-neighbors, SVM, etc.)
Which decision boundary type to use (linear, quadratic)
Hyperparameters (e.g. number of neighbors, maximum depth of tree, etc.): parameters you set that change how the learning algorithm works.
So up to now, we’ve covered two parts for classification: fitting the model to training data, then testing the model on unseen data points. But here’s the thing- there’s a shit ton of classifiers to choose from. Even if we focused all our attention on a linear classifier, there’s still the question of whether to use regularization, what kind of boundary to use, etc. How do we know what to choose?
The normal idea would then be to choose the best combination of algorithm/parameters that produces the best accuracy on test data, right? NO. This is because you’d be conceptually fitting your model to your test data now, which is an absolute no-no because the test-data is supposed to be unseen! So the general rule is to leave the test data untouched until our model is finalized: that means we’ve chosen the FINAL algorithm/boundary/parameters and fit it on all our training data already.
We know that training error is the fraction of training points that are not classified correctly, and test error the fraction of correctly classified UNSEEN points. Generally, training and test error are much different from each other. One reason this is the case is outliers: points whose labels are atypical. For example, in our credit card case, someone with a high income and didn’t borrow frequently (low balance) defaulted anyway, which is not what you’d expect. In training, outliers can affect our decision boundary significantly, which subsequently affects test error.
Another example is overfitting, as we discussed previously: we fit our model too close to some pattern in our training data and as a result don’t generalize to new data well. So our training error is very good, but our test error is not.
In particular, hyperparameters themselves can help to regularize our model: in other words, combat overfitting. An example of a hyperparameter is the \(k\) in k-nearest neighbors. Varying \(k\) will lead to different train/test errors, and we can see what kinds:
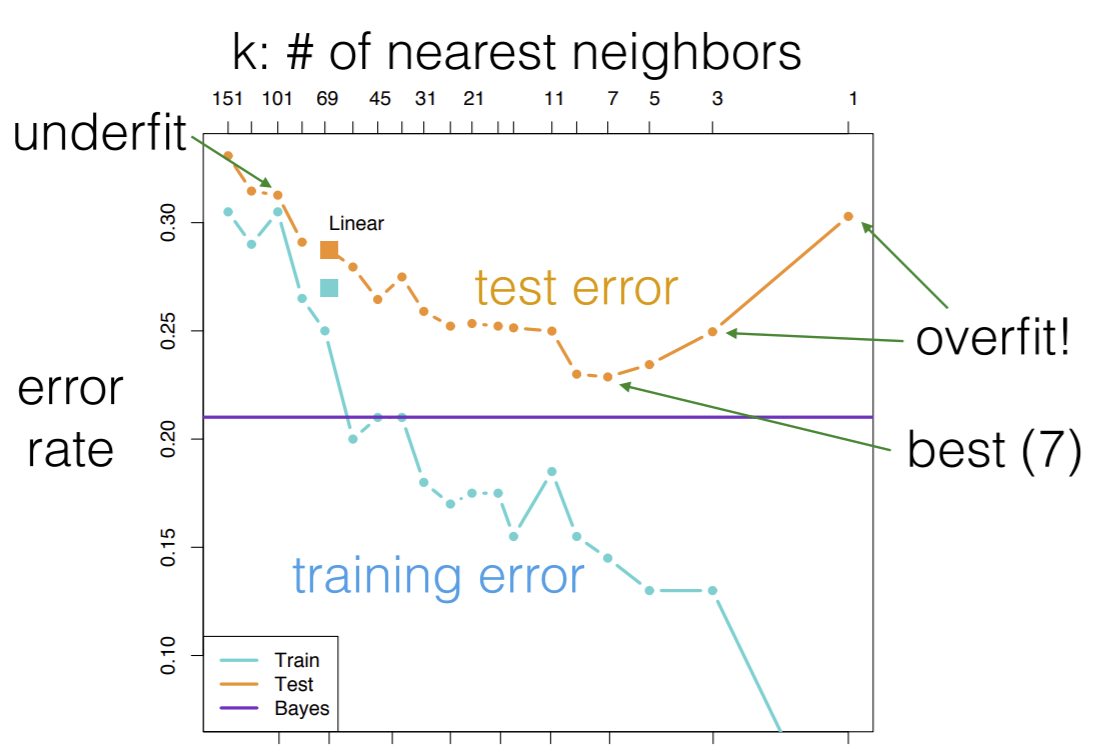
On the x axis we have \(k\) (number of nearest neighbors looked at) and on the y axis we have our error rate. We see both training and test error plotted. We really care more about test error, and see that our optimal hyperparameter is around \(k=7\).
Remember, though, that we can’t use this knowledge when training our model. So instead we have to split the initial training set into a smaller training set and a validation set. We train the classifier on the smaller training set, then use the validation set to get an initial idea of how good our classifier is. The good thing about this is that we can test multiple different models (with variously tuned parameters) using validation. We never, EVER touch the test set until this whole process is done.
So in summary, we now have 3 sets that we derive from all our labeled data:
Training Set: Set used to train model.
Validation Set: Set used for an “initial test” of a built model, and allows us to choose among different models.
Test Set: Set used for the final evaluation of our model. We do not touch it at all until our model is finalized.
